【4.27】LeetCode每日一题· 二叉搜索树的范围和

2021年04月27日 12时03分

标签： LeetCode dfs 树形结构

## 题目描述
给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

#### 示例1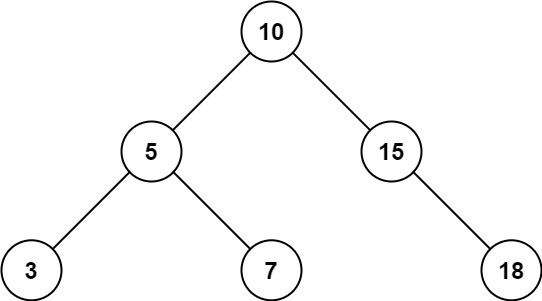
![](https://assets.leetcode.com/uploads/2020/11/05/bst1.jpg)
```
输入：root = [10,5,15,3,7,null,18], low = 7, high = 15
输出：32
```

#### 示例2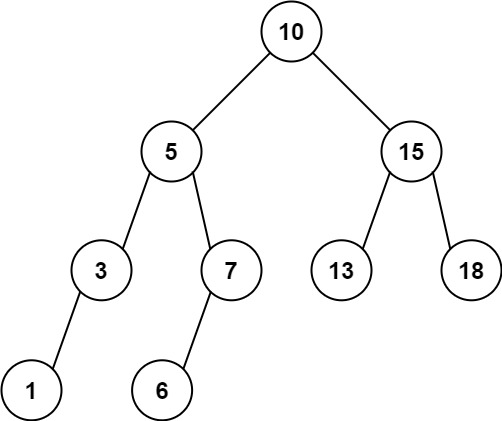
![](https://assets.leetcode.com/uploads/2020/11/05/bst2.jpg)
```
输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出：23
```

#### 提示
```
树中节点数目在范围 [1, 2 * 10^4] 内
1 <= Node.val <= 10^5
1 <= low <= high <= 10^5
所有 Node.val 互不相同
```

#### 来源
> 来源：力扣（LeetCode）
> 链接：[题目链接](https://leetcode-cn.com/problems/range-sum-of-bst "题目链接")

## 解题思路
树的问题一般都使用递归解决。可以直接深度优先遍历整棵二叉树，然后将值在范围内的节点加入答案即可。但是这里没有使用二叉搜索树的特性。

考虑到二叉搜索树某一节点的左子树上的所有节点逗比根节点小，右子树上的所有节点都比根节点大。因此如果某个节点的值已经比`low`小了，那么它左子树上的所有值也一定比`low`小，因此不用遍历其左子树了；同样地，如果某个节点的值已经比`high`大了，那么它右子树上的所有值也一定比`high`大，因此不用遍历其右子树。换句话说，就是只有当某一节点的值大于等于`low`时，才需要遍历其左子树；当值小于等于`high`时，才需要遍历其右子树。因此可以对原来的朴素深度优先搜索做一个剪枝操作。

## 代码
```cpp
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int dfs(TreeNode* root, int low, int high){
        if(!root) return 0;
        int res = 0;
        if(root->val >= low){
            res += dfs(root->left, low, high);
        }
        if(root->val >= low && root->val <= high) res += root->val;
        if(root->val <= high){
            res += dfs(root->right, low, high);
        }
        return res;
    }
    int rangeSumBST(TreeNode* root, int low, int high) {
        return dfs(root, low, high);
    }
};
```

### 用时和内存
> 执行用时：144 ms，在所有 C++提交中击败了69.87%的用户
> 内存消耗：63.1 MB，在所有 C++提交中击败了40.36%的用户

所有评论

暂无评论

新增评论

邮箱

邮箱仅作验证使用

图形验证码

邮箱验证码

目录

【4.27】LeetCode每日一题· 二叉搜索树的范围和

所有评论

暂无评论

新增评论