【4.22】LeetCode每日一题· 矩形区域不超过 K 的最大数值和

2021年04月22日 12时10分

标签： LeetCode 前缀和二分

## 题目描述
给你一个 m x n 的矩阵 matrix 和一个整数 k ，找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。

题目数据保证总会存在一个数值和不超过 k 的矩形区域。

#### 示例1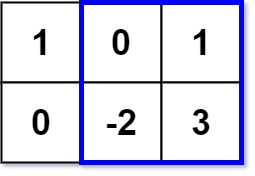
![](https://assets.leetcode.com/uploads/2021/03/18/sum-grid.jpg)
```
输入：matrix = [[1,0,1],[0,-2,3]], k = 2
输出：2
解释：蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。
```

#### 示例2
```
输入：matrix = [[2,2,-1]], k = 3
输出：3
```

#### 提示
```
m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-100 <= matrix[i][j] <= 100
-10^5 <= k <= 10^5
```

#### 来源
> 来源：力扣（LeetCode）
> 链接：[题目链接](https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k "题目链接")

## 解题思路
### 二维前缀和+暴力
一个很直观的想法是，我们在**O(mn)**内预处理出`matrix`的前缀和，然后枚举内部矩形的左上角坐标和右上角坐标，可以在**O(1)**时间内算出内部矩形的元素和，然后和**k**比较并记录答案即可。枚举花费时间为$$O(m^2n^2)$$$，因此最后总的时间复杂度为$$O(mn+m^2n^2)=O(m^2n^2)$$。
Tips：
1. 如果使用`vector`存前缀和会超时，建议直接用数组存；
2. 一个简单的优化：如果当前保存的答案已经和`k`相等了，说明已经不会有更优的答案了，直接返回即可。
### 代码
```cpp
class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
        const int M = matrix.size(), N = matrix[0].size();
        int preSum[M][N];
        for(int i = 0; i < M; i++){
            for(int j = 0; j < N; j++){
                preSum[i][j] = matrix[i][j];
                if(i-1 >= 0){
                    preSum[i][j] += preSum[i-1][j];
                }
                if(j-1 >= 0){
                    preSum[i][j] += preSum[i][j-1];
                }
                if(i-1 >= 0 && j-1 >= 0){
                    preSum[i][j] -= preSum[i-1][j-1];
                }
            }
        }
        
        int temp, res = -INT_MAX;
        for(int x1 = 0; x1 < M; x1++){
            for(int y1 = 0; y1 < N; y1++){
                for(int x2 = x1; x2 < M; x2++){
                    for(int y2 = y1; y2 < N; y2++){

temp = preSum[x2][y2];;
                        if(x1-1 >= 0){
                            temp -= preSum[x1-1][y2];
                        }
                        if(y1-1 >= 0){
                            temp -= preSum[x2][y1-1];
                        }
                        if(x1-1 >= 0 && y1-1 >= 0){
                            temp += preSum[x1-1][y1-1];
                        }

if(temp <= k){
                            res = max(res, temp);
                            if(res == k) return k;
                        }
                    }
                }
            }
        }
        return res;
    }
};
```

### 用时和内存
> 执行用时：428 ms，在所有 C++提交中击败了65.22%的用户
> 内存消耗：8 MB，在所有 C++提交中击败了99.24%的用户

### 一维前缀和+二分
如果我们枚举内部矩形的上下边界，并将每一列的和都算出来，则可以将二维矩阵压缩为一个一维矩阵，我们对该矩阵计算前缀和，记为`preSum[N]`
那么某一区间`[l, r]`的和就可以计算为`preSum[r] - preSum[l-1]`，该值需要小于等于`k`，也就是`preSum[l-1] >= preSum[r] - k (l <= r)`，所以我们可以继续枚举`r`，然后维护一个`preSum`的有序集合，就可以在$$O(log n)$$的时间内找到`l-1`是否存在，如果找到，则更新答案为原答案和`preSum[r] - preSum[l-1]`中的大值即可。

PS：STL还是比较慢的。

### 代码
```cpp
class Solution {
public:
    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
        const int M = matrix.size(), N = matrix[0].size();
        int preSum[N], sum[N], res = -INT_MAX;
        for(int x1 = 0; x1 < M; x1++){
            memset(sum, 0, sizeof(sum));
            for(int x2 = x1; x2 < M; x2++){
                for(int y = 0; y < N; y++){
                    sum[y] += matrix[x2][y];
                    preSum[y] = sum[y] + (y-1>=0? preSum[y-1]: 0);
                }
                set<int> st{0};
                for(int i = 0; i < N; i++){
                    auto sj = st.lower_bound(preSum[i]-k);
                    if(sj != st.end()){
                        res = max(res, preSum[i] - *sj);
                    }
                    st.insert(preSum[i]);
                }
            }
        }
        return res;
    }
};
```

### 用时和内存
> 执行用时：592 ms，在所有 C++提交中击败了38.94%的用户
> 内存消耗：127.9 MB，在所有 C++提交中击败了9.84%的用户

所有评论

暂无评论

新增评论

邮箱

邮箱仅作验证使用

图形验证码

邮箱验证码

目录

【4.22】LeetCode每日一题· 矩形区域不超过 K 的最大数值和

所有评论

暂无评论

新增评论