【2024.04.11】LeetCode每日一题·互质树

2024年04月11日 21时33分

标签： LeetCode 哈希表 dfs 树形结构 Hard

## 题目描述

给你一个`n`个节点的树（也就是一个无环连通无向图），节点编号从`0`到`n - 1`，且恰好有`n - 1`条边，每个节点有一个值。树的**根节点**为`0`号点。

给你一个整数数组`nums`和一个二维数组`edges`来表示这棵树。`nums[i]`表示第`i`个点的值，`edges[j] = [u_j, v_j]`表示节点`u_j`和节点`v_j`在树中有一条边。

当`gcd(x, y) == 1`，我们称两个数`x`和`y`是**互质的**，其中`gcd(x, y)`是`x`和`y`的**最大公约数**。

从节点`i`到**根**最短路径上的点都是节点`i`的祖先节点。一个节点**不是**它自己的祖先节点。

请你返回一个大小为`n`的数组`ans`，其中`ans[i]`是离节点`i`最近的祖先节点且满足`nums[i]`和`nums[ans[i]]`是**互质的**，如果不存在这样的祖先节点，`ans[i]`为**-1**。

#### 示例1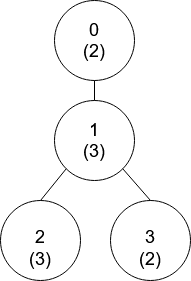
![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2021/02/20/untitled-diagram.png)
````
输入：nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
输出：[-1,0,0,1]
解释：上图中，每个节点的值在括号中表示。
- 节点 0 没有互质祖先。
- 节点 1 只有一个祖先节点 0 。它们的值是互质的（gcd(2,3) == 1）。
- 节点 2 有两个祖先节点，分别是节点 1 和节点 0 。节点 1 的值与它的值不是互质的（gcd(3,3) == 3）但节点 0 的值是互质的(gcd(2,3) == 1)，所以节点 0 是最近的符合要求的祖先节点。
- 节点 3 有两个祖先节点，分别是节点 1 和节点 0 。它与节点 1 互质（gcd(3,2) == 1），所以节点 1 是离它最近的符合要求的祖先节点。
````

#### 示例2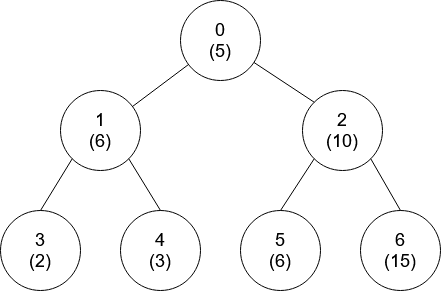
![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2021/02/20/untitled-diagram1.png)
````
输入：nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出：[-1,0,-1,0,0,0,-1]
````

#### 提示
````
nums.length == n
1 <= nums[i] <= 50
1 <= n <= 10^5
edges.length == n - 1
edges[j].length == 2
0 <= u_j, v_j < n
u_j != v_j
````

#### 来源

> 来源：力扣（LeetCode）
> 
> 链接：[1766. 互质树](https://leetcode.cn/problems/tree-of-coprimes/description/)

## 解题思路
注意到从根节点到某一节点的最短路径，就是深度优先搜索（DFS）从根节点搜索到这一节点的路径，因此所要求的答案肯定在这一段路径上。接下来的问题就在于如何在这一段路径上找到距离目标节点最近的、且其值与目标节点互质的节点。

如果直接遍历当前路径上的所有节点，则在最坏状态下（树退化成了链状结构）需要重新遍历所有的节点，时间复杂度为$$O(n^2)$$，不符合数据范围的要求。

考虑到节点值的数据范围仅为`1 <= nums[i] <= 50`，因此可以预处理好所有与可能的节点值互质的值。然后查找与当前节点互质的值是否在当前路径中出现即可，最终答案就是：当前路径中，所有与【当前节点互质的值对应的节点】中，取距离当前节点最近的节点（换句话说，最后遍历到的节点）。这一操作可以直接使用哈希表记录`{节点值：[(节点0，位置0), (节点1，位置1)...]}`来实现（实际操作用由于`nums[i]`是整数，因此直接用顺序表实现即可）。由于路径是从远到近搜索的，因此对于每个互质的值对应的节点列表，出现在最后一个位置的节点一定是后遍历到的。因此在比较不同互质的值对应的节点时，只需要比较节点列表最后一个节点的位置即可。这样就可以在时间复杂度$$O(50\cdot n)$$之内实现。

代码中需要注意的是，输入中给出的边是有向的，但实际需要的是无向边，因此在建图的时候需要注意。

## 代码
````cpp
class Solution {
private:
    vector<vector<int>> g; // 建图
    vector<int> vis;
    vector<int> ans;
    vector<vector<pair<int, int>>> path; // 当前经过的路径的value: [{id, dps}]对
    vector<vector<int>> primes; // primes[num] := 所有与num互为质数的数
public:
    int gcd(int a, int b) {
        return b > 0 ? gcd(b, a%b): a;
    }

void getPrimes(void){
        for(int i = 0; i <= 50; i++){
            primes.push_back(vector<int>());
            if(i == 0) continue;
            for(int j = 0; j <= 50; j++){
                if(gcd(i, j) == 1){
                    primes[i].push_back(j);
                }
            }
        }
    }

void dfs(int root, int dps, vector<int>& nums){
        int value = nums[root];
        int opt_dps = -1, opt_res = -1;
        for(int v: primes[value]){
            vector<pair<int, int>>& nodes = path[v];
            if(!nodes.size()) continue;
            int res = nodes[nodes.size()-1].first, dps = nodes[nodes.size()-1].second;
            if(dps > opt_dps){
                opt_dps = dps;
                opt_res = res;
            }
        }
        ans[root] = opt_res;
        path[value].push_back(pair<int, int>(root, dps));
        vis[root] = true;
        for(int to: g[root]){
            if(vis[to]) continue;
            dfs(to, dps+1, nums);
        }
        vis[root] = false;
        path[value].pop_back();
        return;
    }
    vector<int> getCoprimes(vector<int>& nums, vector<vector<int>>& edges) {
        const int N = nums.size();
        g.resize(N);
        vis.resize(N, false);
        ans.resize(N, -1);
        path.resize(51);

getPrimes(); // 预处理每个值的互质数
        // 建图
        for(vector<int>& e: edges){
            int u = e[0], v = e[1];
            g[u].push_back(v);
            g[v].push_back(u);
        }
        dfs(0, 0, nums);
        return ans;
    }
};
````

## 用时和内存
> 执行用时：1303 ms，在所有C++提交中击败了27.38%的用户
>
> 内存消耗：174.32 MB，在所有C++提交中击败51.19%的用户
>

所有评论

暂无评论

新增评论

邮箱

邮箱仅作验证使用

图形验证码

邮箱验证码

目录

【2024.04.11】LeetCode每日一题·互质树

所有评论

暂无评论

新增评论